
Typically the projectile's energy is known due to weight and velocity. There are four factors in calculating applied energy: projectile energy projectile construction projectile sectional density and target construction. Again, the bullet weight remaining the same. However, in this case if the bullet is bigger or smaller in caliber then the penetration will be different due to the change in sectional density. The energy at the muzzle, downrange, or at the point of impact will be the same. If using a bullet as an example, it does not matter how big the bullet is (size in caliber as long as it still weighs the same) or how big the target is. The problem with trying to apply energy to penetration and or effectiveness is that energy is a base unit or constant. Also, not only will the lead ball possess the same energy, but it will possess the same ability to penetration. The difference is throwing and shooting are artificial means of accelerating the lead ball where as dropping it is a natural means of accelerating it. Whether you drop 1 ounce lead ball, throw it or shoot it from a gun, if it has the same velocity it will have the same energy. The energy of a projectile is a calculation based in the acceleration of gravity here on earth, which is 9.80665 meters per second or 32.1739 feet per second. Projectile: monolithic solid type bullet weighing 300 grains with a muzzle velocity of 2900 feet per second. Muzzle energy = bullet mass x bullet velocity 2 / ( 2 x dimensional constant x 7000 ).įirearm: Weatherby Mark V chambered in. Projectile: monolithic solid type bullet weighing 19.5 grams with a muzzle velocity of 884 meters per second. Muzzle energy = ½ x bullet mass x bullet velocity 2 / 1000.įirearm: Weatherby Mark V chambered in.

Here are the two formulas for a calculation of, or more correctly the measurement of muzzle energy. Muzzle energy is calculated by using the known velocity and weight of a projectile.
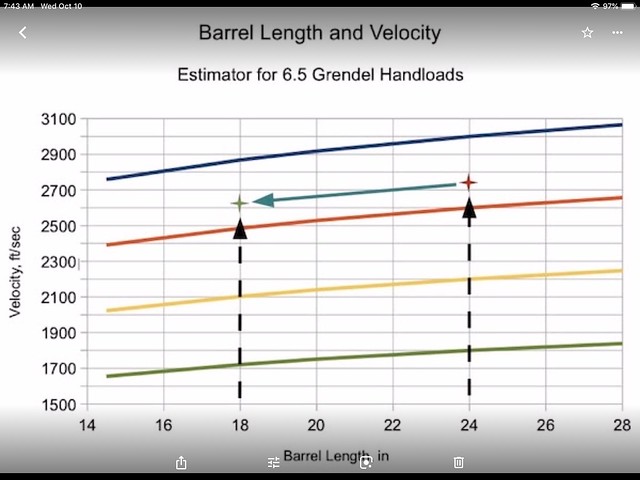
#MUZZLE VELOCITY CALCULATOR FULL#
Which means I can’t define a distance on rails, because the discharge time of the capacitor doesn’t match the exact time the projectile needs to cross the full length of the rails.

I can’t just put the current as a function of a discharging capacitor, because it gives me a time in which the capacitor discharge and this is equal to the time the projectile can accelerate on the rails. The capacitor discharge formula for capacitors is:I = (V_0/R) * e^() The problem is, I am using capacitors and the discharge current isn’t constant with capacitors.
#MUZZLE VELOCITY CALCULATOR FREE#


 0 kommentar(er)
0 kommentar(er)
